EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks

Authors: Mingxing Tan$^{1}$, Quoc V. Le$^{1}$

$^{1}$Google Research, Brain Team, Mountain View, CA

Correspondence to: Mingxing Tan [email protected]

Proceedings of the 36$^{\text{th}}$ International Conference on Machine Learning, Long Beach, California, PMLR 97, 2019.

Abstract

Section Summary: This paper explores how to improve convolutional neural networks, or ConvNets, by scaling them up more effectively, finding that balancing the network's depth, width, and image resolution leads to better accuracy without wasting resources. The authors introduce a simple scaling technique that evenly adjusts all three dimensions using a compound coefficient, which boosts performance on models like MobileNets and ResNet. They go further by designing a new baseline network through automated search and scaling it into the EfficientNets family, where the top model achieves top accuracy on image recognition tasks while being much smaller and faster than competitors, and it also excels on other datasets with fewer parameters.

Convolutional Neural Networks (ConvNets) are commonly developed at a fixed resource budget, and then scaled up for better accuracy if more resources are available. In this paper, we systematically study model scaling and identify that carefully balancing network depth, width, and resolution can lead to better performance. Based on this observation, we propose a new scaling method that uniformly scales all dimensions of depth/width/resolution using a simple yet highly effective compound coefficient. We demonstrate the effectiveness of this method on scaling up MobileNets and ResNet.

To go even further, we use neural architecture search to design a new baseline network and scale it up to obtain a family of models, called EfficientNets, which achieve much better accuracy and efficiency than previous ConvNets. In particular, our EfficientNet-B7 achieves state-of-the-art 84.3% top-1 accuracy on ImageNet, while being 8.4x smaller and 6.1x faster on inference than the best existing ConvNet. Our EfficientNets also transfer well and achieve state-of-the-art accuracy on CIFAR-100 (91.7%), Flowers (98.8%), and 3 other transfer learning datasets, with an order of magnitude fewer parameters. Source code is at https://github.com/tensorflow/tpu/tree/master/models/official/efficientnet.

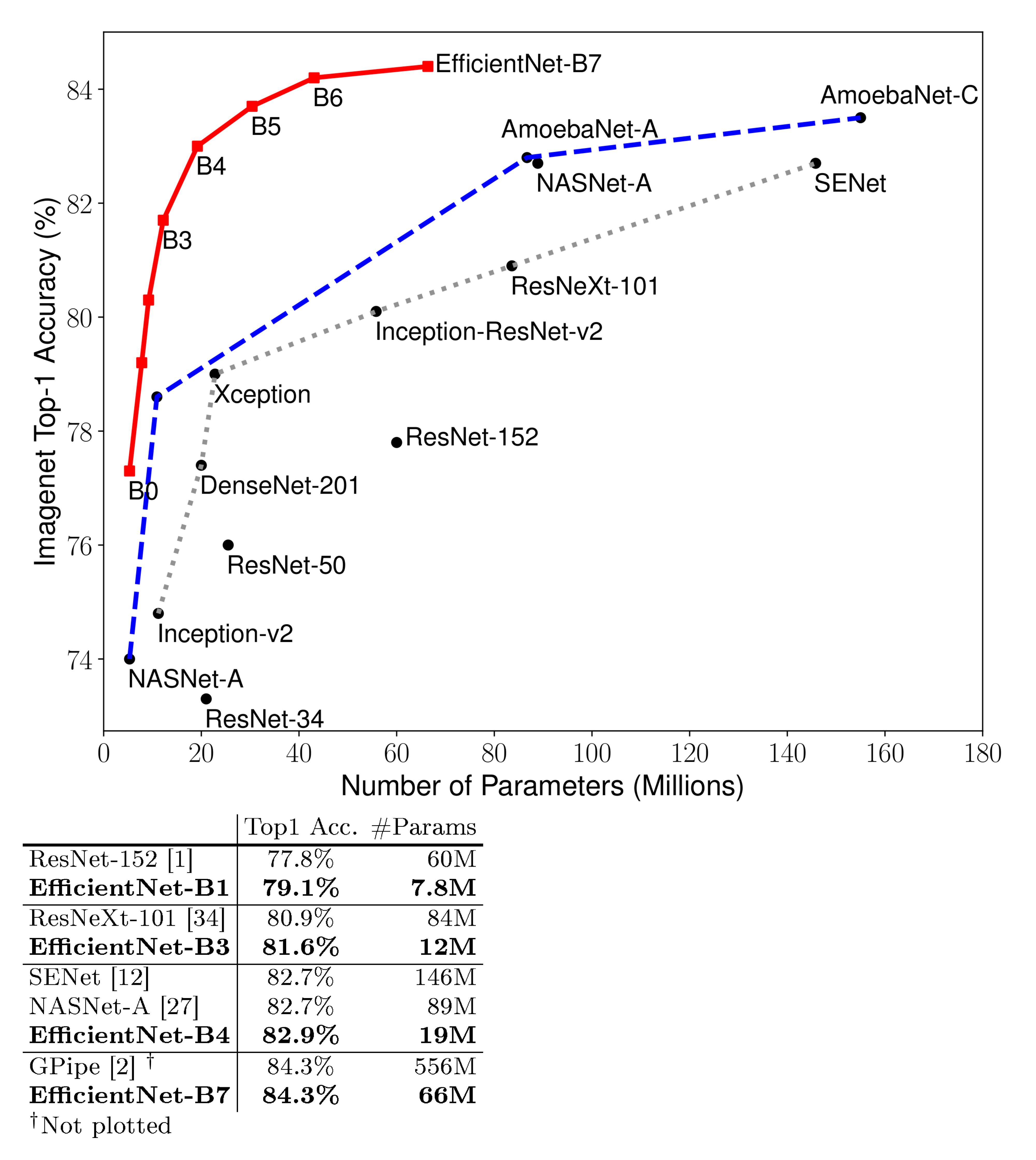
Executive Summary: Convolutional neural networks, or ConvNets, power much of modern image recognition technology, from smartphone cameras to medical diagnostics. However, as these models grow larger to boost accuracy, they demand enormous computational resources, hitting hardware limits and driving up costs for training and deployment. This inefficiency hampers widespread adoption, especially on resource-constrained devices like mobiles or in real-time applications. With data volumes exploding and AI integrating into everyday tools, the need for accurate yet efficient models has never been more urgent.

This paper sets out to rethink how ConvNets are scaled up for better performance. It evaluates whether balancing the network's depth (number of layers), width (number of channels per layer), and input resolution (image size) can yield higher accuracy with fewer resources, compared to traditional methods that scale just one dimension.

The authors conducted an empirical study using existing ConvNets like MobileNets and ResNet, analyzing how changes in depth, width, and resolution affect accuracy under controlled resource budgets, measured by floating-point operations (FLOPS). They drew from large datasets like ImageNet, which contains over a million labeled images across 1,000 classes, and tested over several months on standard hardware. Key assumptions included uniform scaling across layers and a focus on convolution operations, which dominate computation. Building on this, they used neural architecture search—a method that automates network design—to create a compact baseline model, then applied their proposed "compound scaling" method, which proportionally increases all three dimensions using fixed ratios tuned via a small grid search on the baseline.

The study uncovered three main findings. First, traditional single-dimension scaling, such as deepening layers or widening channels, improves accuracy but yields diminishing returns and wastes resources; for instance, quadrupling depth on ResNet-50 raised accuracy by just 2.1 percentage points at four times the FLOPS. Second, their compound scaling method boosts accuracy more effectively; scaling MobileNetV2 this way improved ImageNet accuracy to 77.4% versus 76.8% from depth-only scaling, using similar FLOPS. Third, applying compound scaling to their new baseline produced the EfficientNet family, where the largest model, EfficientNet-B7, hit 84.3% top-1 accuracy on ImageNet—matching the prior state-of-the-art—while using 8.4 times fewer parameters (66 million versus 557 million) and running 6.1 times faster on CPU inference.

These results mean ConvNets can achieve top performance without the bloat that strains hardware and budgets. EfficientNets cut parameters by up to 21 times compared to rivals like NASNet on similar tasks, slashing training costs and enabling deployment on everyday devices. They also excel in transfer learning, setting new records on five of eight datasets (e.g., 98.8% on Flowers versus prior 98.5%), with 9.6 times fewer parameters on average, which reduces risks in applications like autonomous vehicles or healthcare where speed and reliability matter. This outperforms expectations from prior work, which focused on one-off tweaks, by showing balanced scaling unlocks efficiency gains that prior oversized models overlooked.

Leaders should prioritize EfficientNet architectures for upcoming AI projects, especially those involving image analysis, to optimize performance per resource dollar. For resource-rich environments, scale to EfficientNet-B7; for mobiles, start with smaller variants like B0. Trade-offs include slightly higher upfront design effort via architecture search, but gains in speed and cost justify it. Further work, such as piloting on specific hardware or integrating with object detection tasks, would refine adaptations before full rollout.

While robust across benchmarks, limitations include reliance on ImageNet-style training data, which may not generalize to all real-world scenarios, and results tuned for general FLOPS rather than device-specific latency. Confidence in the core claims is high, backed by direct comparisons and hardware tests, though caution is advised for non-standard datasets where more validation data might be needed.

1. Introduction

Section Summary: Scaling up convolutional neural networks, or ConvNets, which are AI models used for tasks like image recognition, typically improves accuracy by increasing their depth, width, or the resolution of input images, but these approaches often lack balance and require manual tweaking for optimal results. This paper explores a more principled way to scale these models by evenly adjusting depth, width, and resolution using fixed ratios determined from a small initial model, a method called compound scaling that intuitively accommodates larger inputs with deeper layers and more channels. The approach works well on existing models like ResNet and leads to a new family called EfficientNets, which achieve top performance on ImageNet and other datasets with far fewer parameters and faster speeds than previous top models.

Scaling up ConvNets is widely used to achieve better accuracy. For example, ResNet [1] can be scaled up from ResNet-18 to ResNet-200 by using more layers; Recently, GPipe [2] achieved 84.3% ImageNet top-1 accuracy by scaling up a baseline model four time larger. However, the process of scaling up ConvNets has never been well understood and there are currently many ways to do it. The most common way is to scale up ConvNets by their depth [1] or width [3]. Another less common, but increasingly popular, method is to scale up models by image resolution [2]. In previous work, it is common to scale only one of the three dimensions – depth, width, and image size. Though it is possible to scale two or three dimensions arbitrarily, arbitrary scaling requires tedious manual tuning and still often yields sub-optimal accuracy and efficiency.

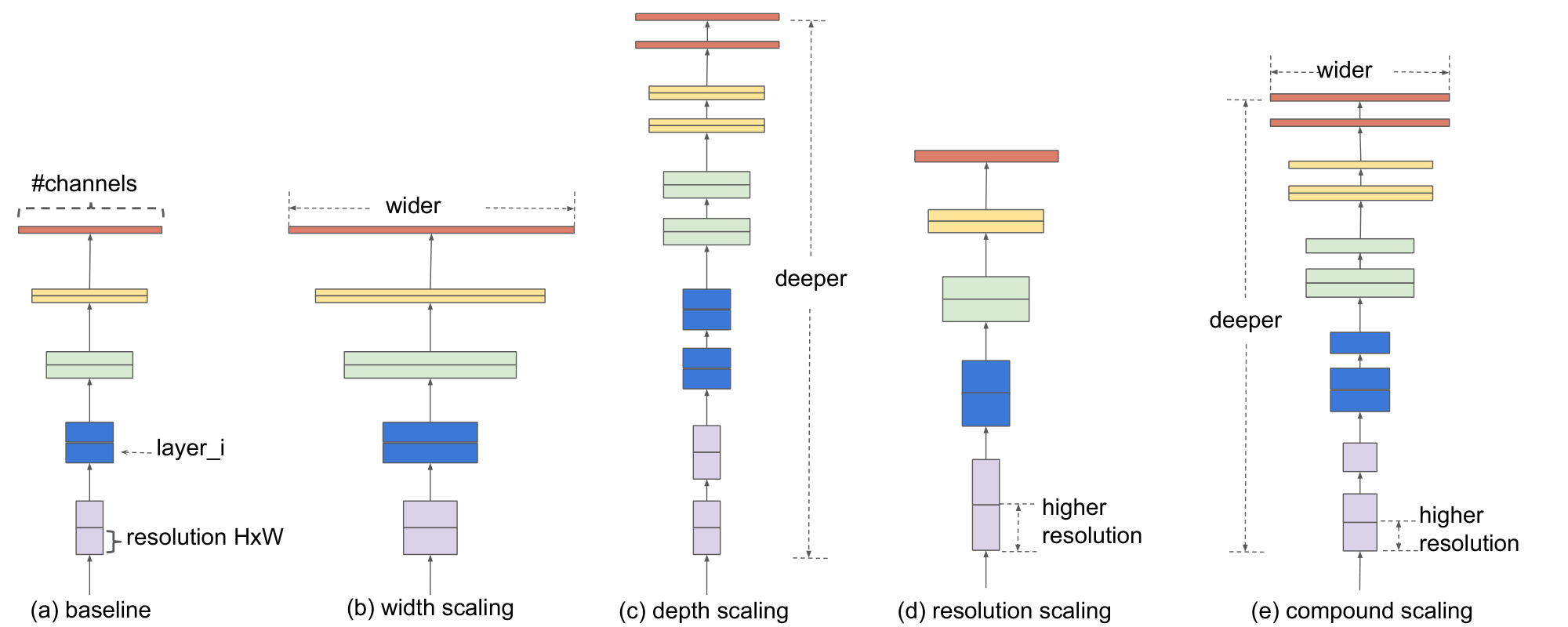
In this paper, we want to study and rethink the process of scaling up ConvNets. In particular, we investigate the central question: is there a principled method to scale up ConvNets that can achieve better accuracy and efficiency? Our empirical study shows that it is critical to balance all dimensions of network width/depth/resolution, and surprisingly such balance can be achieved by simply scaling each of them with constant ratio. Based on this observation, we propose a simple yet effective compound scaling method. Unlike conventional practice that arbitrary scales these factors, our method uniformly scales network width, depth, and resolution with a set of fixed scaling coefficients. For example, if we want to use $2^N$ times more computational resources, then we can simply increase the network depth by $\alpha ^ N$, width by $\beta ^ N$, and image size by $\gamma ^ N$, where $\alpha, \beta, \gamma$ are constant coefficients determined by a small grid search on the original small model. Figure 2 illustrates the difference between our scaling method and conventional methods.

Intuitively, the compound scaling method makes sense because if the input image is bigger, then the network needs more layers to increase the receptive field and more channels to capture more fine-grained patterns on the bigger image. In fact, previous theoretical [4, 5] and empirical results [3] both show that there exists certain relationship between network width and depth, but to our best knowledge, we are the first to empirically quantify the relationship among all three dimensions of network width, depth, and resolution.

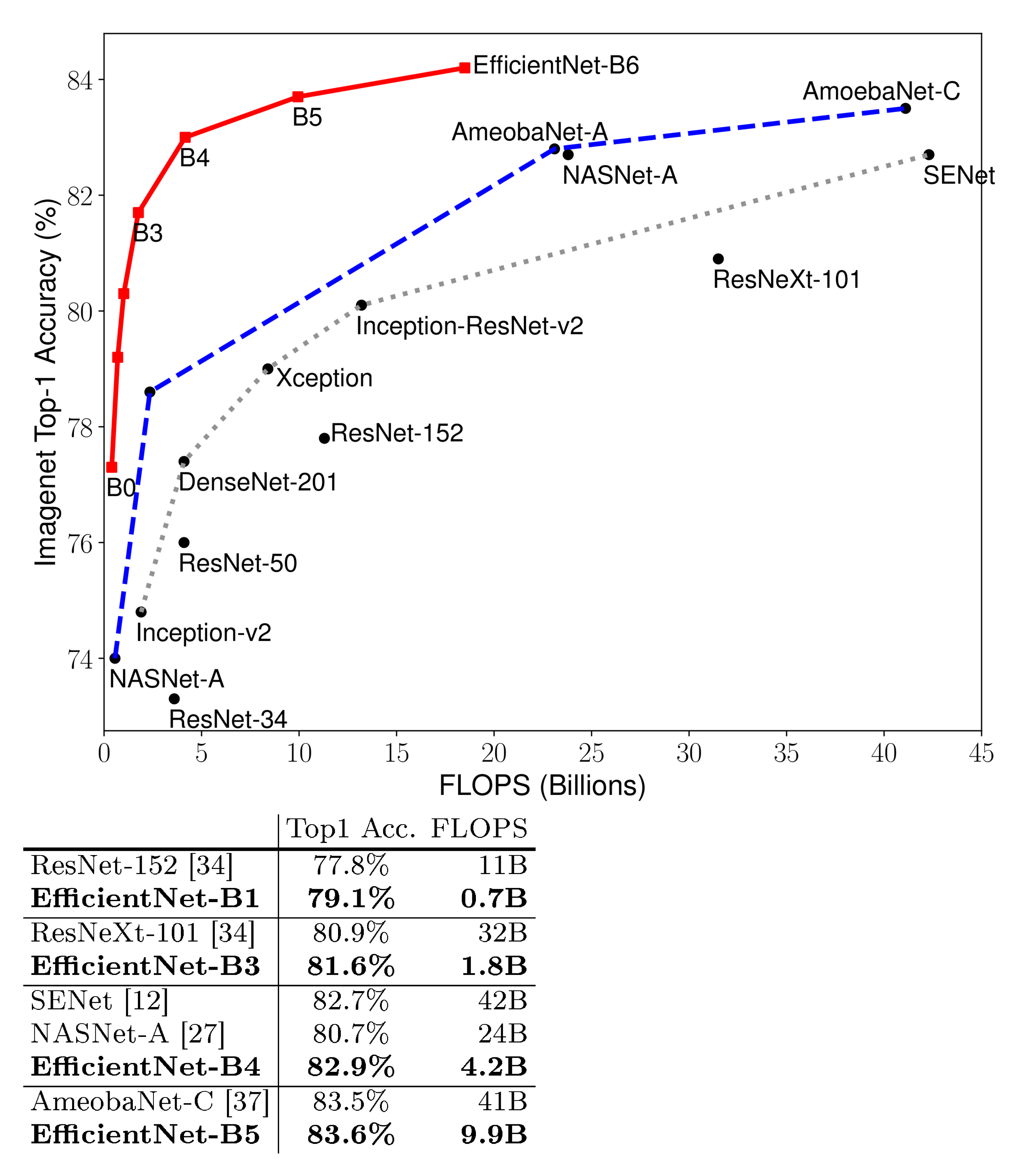
We demonstrate that our scaling method work well on existing MobileNets [6, 7] and ResNet [1]. Notably, the effectiveness of model scaling heavily depends on the baseline network; to go even further, we use neural architecture search [8, 9] to develop a new baseline network, and scale it up to obtain a family of models, called EfficientNets. Figure 1 summarizes the ImageNet performance, where our EfficientNets significantly outperform other ConvNets. In particular, our EfficientNet-B7 surpasses the best existing GPipe accuracy [2], but using 8.4x fewer parameters and running 6.1x faster on inference. Compared to the widely used ResNet-50 [1], our EfficientNet-B4 improves the top-1 accuracy from 76.3% to 83.0% (+6.7%) with similar FLOPS. Besides ImageNet, EfficientNets also transfer well and achieve state-of-the-art accuracy on 5 out of 8 widely used datasets, while reducing parameters by up to 21x than existing ConvNets.

2. Related Work

Section Summary: Since the breakthrough of AlexNet in 2012, convolutional neural networks have dramatically improved in accuracy on image recognition tasks by becoming larger and more complex, with recent models boasting over 80% accuracy on benchmark datasets but straining computer hardware limits. To make these networks more efficient, especially for devices like smartphones, researchers have developed compression techniques, hand-designed lightweight models, and automated search methods, though applying them to massive high-accuracy networks remains challenging. The paper explores scaling these networks by adjusting their depth, width, and input resolution to balance better performance with practical efficiency, building on prior studies that highlight the importance of these dimensions.

**ConvNet Accuracy: **

Since AlexNet [10] won the 2012 ImageNet competition, ConvNets have become increasingly more accurate by going bigger: while the 2014 ImageNet winner GoogleNet [11] achieves 74.8% top-1 accuracy with about 6.8M parameters, the 2017 ImageNet winner SENet [12] achieves 82.7% top-1 accuracy with 145M parameters. Recently, GPipe [2] further pushes the state-of-the-art ImageNet top-1 validation accuracy to 84.3% using 557M parameters: it is so big that it can only be trained with a specialized pipeline parallelism library by partitioning the network and spreading each part to a different accelerator. While these models are mainly designed for ImageNet, recent studies have shown better ImageNet models also perform better across a variety of transfer learning datasets [13], and other computer vision tasks such as object detection [1, 9]. Although higher accuracy is critical for many applications, we have already hit the hardware memory limit, and thus further accuracy gain needs better efficiency.

**ConvNet Efficiency: **

Deep ConvNets are often over-parameterized. Model compression [14, 15, 16] is a common way to reduce model size by trading accuracy for efficiency. As mobile phones become ubiquitous, it is also common to hand-craft efficient mobile-size ConvNets, such as SqueezeNets [17, 18], MobileNets [6, 7], and ShuffleNets [19, 20]. Recently, neural architecture search becomes increasingly popular in designing efficient mobile-size ConvNets [9, 21], and achieves even better efficiency than hand-crafted mobile ConvNets by extensively tuning the network width, depth, convolution kernel types and sizes. However, it is unclear how to apply these techniques for larger models that have much larger design space and much more expensive tuning cost. In this paper, we aim to study model efficiency for super large ConvNets that surpass state-of-the-art accuracy. To achieve this goal, we resort to model scaling.

**Model Scaling: **

There are many ways to scale a ConvNet for different resource constraints: ResNet [1] can be scaled down (e.g., ResNet-18) or up (e.g., ResNet-200) by adjusting network depth (#layers), while WideResNet [3] and MobileNets [6] can be scaled by network width (#channels). It is also well-recognized that bigger input image size will help accuracy with the overhead of more FLOPS. Although prior studies [4, 22, 23, 5] have shown that network depth and width are both important for ConvNets' expressive power, it still remains an open question of how to effectively scale a ConvNet to achieve better efficiency and accuracy. Our work systematically and empirically studies ConvNet scaling for all three dimensions of network width, depth, and resolutions.

3. Compound Model Scaling

Section Summary: This section explains how to scale up convolutional neural networks, or ConvNets, by adjusting their depth, width, or input resolution to improve accuracy while staying within limits on memory and computation. It notes that increasing any one of these aspects boosts performance initially but yields smaller gains as the model grows larger, based on studies of existing networks like ResNet. To address how these factors influence each other—for instance, higher-resolution images needing deeper and wider networks—the authors propose a combined scaling approach that adjusts all dimensions together for better results.

In this section, we will formulate the scaling problem, study different approaches, and propose our new scaling method.

3.1 Problem Formulation

A ConvNet Layer $i$ can be defined as a function: $Y_i = \mathcal{F}_i(X_i)$, where $\mathcal{F}_i$ is the operator, $Y_i$ is output tensor, $X_i$ is input tensor, with tensor shape $\langle H_i, W_i, C_i \rangle$ [^1], where $H_i$ and $W_i$ are spatial dimension and $C_i$ is the channel dimension. A ConvNet $\mathcal{N}$ can be represented by a list of composed layers: $\mathcal{N} = \mathcal{F}_k \odot ... \odot \mathcal{F}_2 \odot \mathcal{F}1 (X_1) = \bigodot{j=1...k} \mathcal{F}_j (X_1)$. In practice, ConvNet layers are often partitioned into multiple stages and all layers in each stage share the same architecture: for example, ResNet [1] has five stages, and all layers in each stage has the same convolutional type except the first layer performs down-sampling. Therefore, we can define a ConvNet as:

[^1]: For the sake of simplicity, we omit batch dimension.

$ \mathcal{N} = \bigodot_{i=1...s} \mathcal{F}{i}^{L_i} \big(X{\langle H_i, W_i, C_i \rangle}\big) $

where $\mathcal{F}{i}^{L_i}$ denotes layer $F{i}$ is repeated $L_i$ times in stage $i$, $\langle H_i, W_i, C_i \rangle$ denotes the shape of input tensor $X$ of layer $i$. Figure 2(a) illustrate a representative ConvNet, where the spatial dimension is gradually shrunk but the channel dimension is expanded over layers, for example, from initial input shape $\langle 224, 224, 3 \rangle$ to final output shape $\langle 7, 7, 512 \rangle$.

Unlike regular ConvNet designs that mostly focus on finding the best layer architecture $\mathcal{F}_i$, model scaling tries to expand the network length ($L_i$), width ($C_i$), and/or resolution ($H_i, W_i$) without changing $\mathcal{F}_i$ predefined in the baseline network. By fixing $\mathcal{F}_i$, model scaling simplifies the design problem for new resource constraints, but it still remains a large design space to explore different $L_i, C_i, H_i, W_i$ for each layer. In order to further reduce the design space, we restrict that all layers must be scaled uniformly with constant ratio. Our target is to maximize the model accuracy for any given resource constraints, which can be formulated as an optimization problem:

$ \begin{aligned} &\operatorname*{max}{d, w, r} & &Accuracy \big(\mathcal{N}(d, w, r)\big) \ &s.t. & & \mathcal{N}(d, w, r) = \bigodot{i=1...s} \mathcal{\hat F}{i}^{d\cdot \hat L_i} \big(X{ \langle r\cdot \hat H_i, r\cdot \hat W_i, w\cdot \hat C_i \rangle}\big) \ & && \text{Memory}(\mathcal{N}) \le \text{target_memory} \ &&& \text{FLOPS}(\mathcal{N}) \le \text{target_flops} \ \end{aligned}\tag{1} $

where $w, d, r$ are coefficients for scaling network width, depth, and resolution; $\mathcal{\hat F}_i, \hat L_i, \hat H_i, \hat W_i, \hat C_i$ are predefined parameters in baseline network (see Table 1 as an example).

3.2 Scaling Dimensions

The main difficulty of problem Equation 1 is that the optimal $d, w, r$ depend on each other and the values change under different resource constraints. Due to this difficulty, conventional methods mostly scale ConvNets in one of these dimensions:

**Depth ($\pmb d$): **

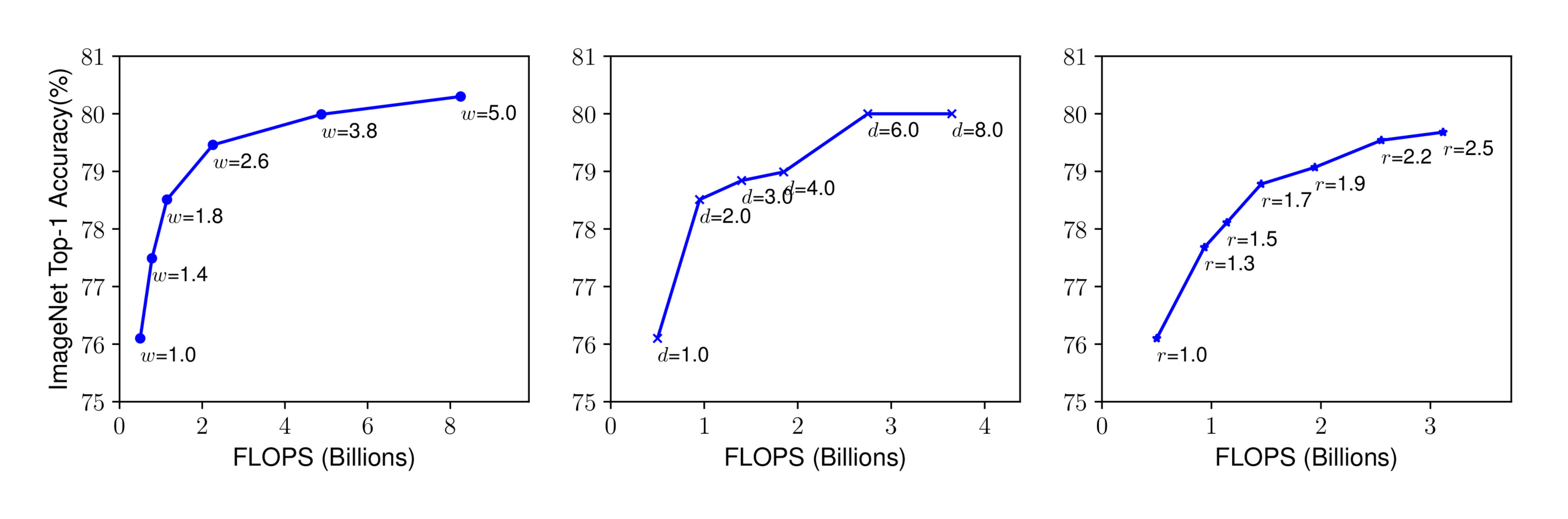
Scaling network depth is the most common way used by many ConvNets [1, 24, 11, 25]. The intuition is that deeper ConvNet can capture richer and more complex features, and generalize well on new tasks. However, deeper networks are also more difficult to train due to the vanishing gradient problem [3]. Although several techniques, such as skip connections [1] and batch normalization [26], alleviate the training problem, the accuracy gain of very deep network diminishes: for example, ResNet-1000 has similar accuracy as ResNet-101 even though it has much more layers. Figure 3 (middle) shows our empirical study on scaling a baseline model with different depth coefficient $d$, further suggesting the diminishing accuracy return for very deep ConvNets.

**Width ($\pmb w$): **

Scaling network width is commonly used for small size models [6, 7, 9][^2]. As discussed in [3], wider networks tend to be able to capture more fine-grained features and are easier to train. However, extremely wide but shallow networks tend to have difficulties in capturing higher level features. Our empirical results in Figure 3 (left) show that the accuracy quickly saturates when networks become much wider with larger $w$.

[^2]: In some literature, scaling number of channels is called ``depth multiplier", which means the same as our width coefficient $w$.

**Resolution ($\pmb r$): **

With higher resolution input images, ConvNets can potentially capture more fine-grained patterns. Starting from 224x224 in early ConvNets, modern ConvNets tend to use 299x299 [25] or 331x331 [27] for better accuracy. Recently, GPipe [2] achieves state-of-the-art ImageNet accuracy with 480x480 resolution. Higher resolutions, such as 600x600, are also widely used in object detection ConvNets [28, 29]. Figure 3 (right) shows the results of scaling network resolutions, where indeed higher resolutions improve accuracy, but the accuracy gain diminishes for very high resolutions ($r=1.0$ denotes resolution 224x224 and $r=2.5$ denotes resolution 560x560).

The above analyses lead us to the first observation:

Observation 1 –

Scaling up any dimension of network width, depth, or resolution improves accuracy, but the accuracy gain diminishes for bigger models.

3.3 Compound Scaling

We empirically observe that different scaling dimensions are not independent. Intuitively, for higher resolution images, we should increase network depth, such that the larger receptive fields can help capture similar features that include more pixels in bigger images. Correspondingly, we should also increase network width when resolution is higher, in order to capture more fine-grained patterns with more pixels in high resolution images. These intuitions suggest that we need to coordinate and balance different scaling dimensions rather than conventional single-dimension scaling.

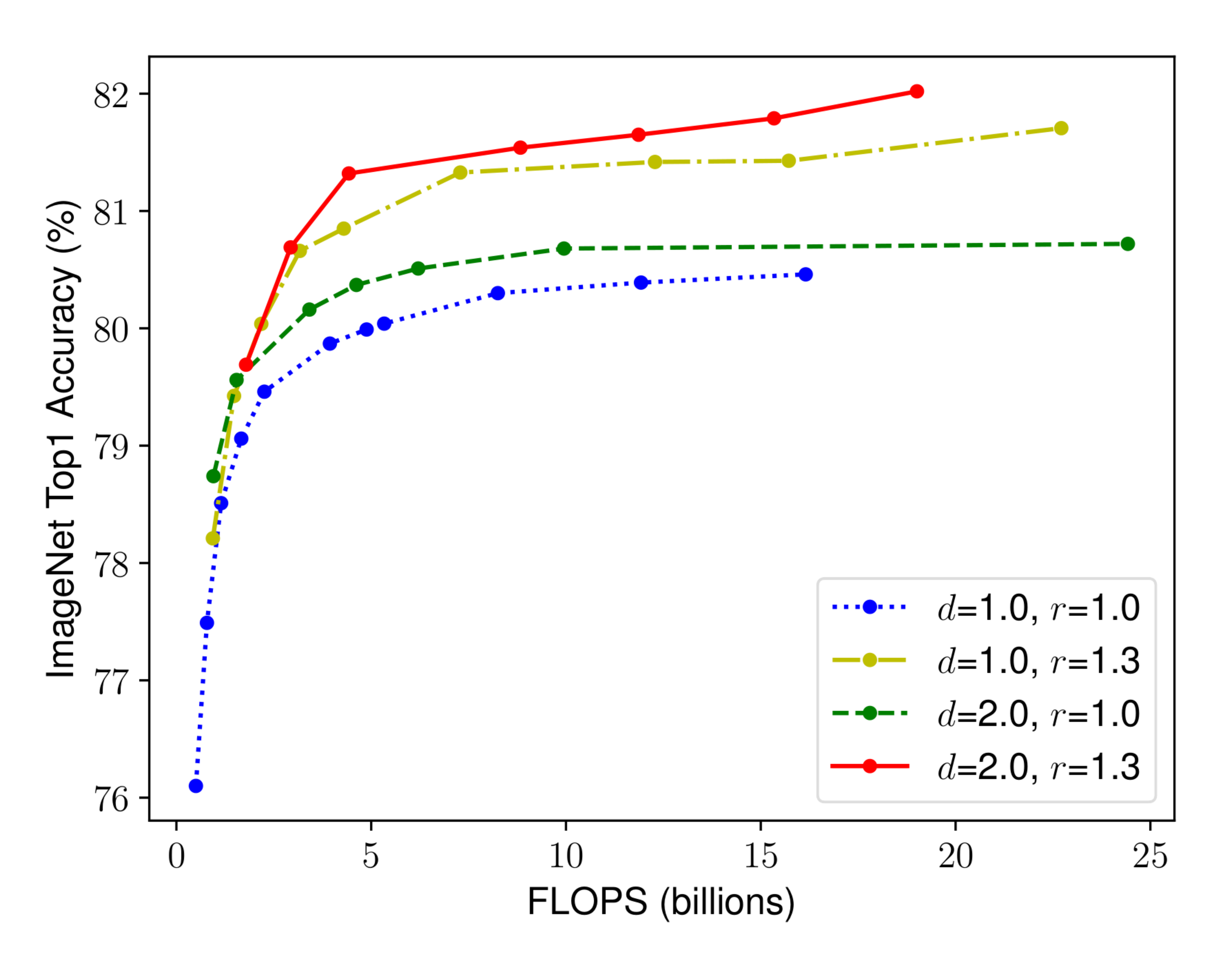
To validate our intuitions, we compare width scaling under different network depths and resolutions, as shown in Figure 4. If we only scale network width $w$ without changing depth ($d$ =1.0) and resolution ($r$ =1.0), the accuracy saturates quickly. With deeper ($d$ =2.0) and higher resolution ($r$ =2.0), width scaling achieves much better accuracy under the same FLOPS cost. These results lead us to the second observation:

Observation 2 –

In order to pursue better accuracy and efficiency, it is critical to balance all dimensions of network width, depth, and resolution during ConvNet scaling.

In fact, a few prior work [27, 30] have already tried to arbitrarily balance network width and depth, but they all require tedious manual tuning.

In this paper, we propose a new compound scaling method, which use a compound coefficient $\phi$ to uniformly scales network width, depth, and resolution in a principled way:

$ \begin{aligned} \text{depth: } & d = \alpha ^ \phi \ \text{width: } & w = \beta ^ \phi \ \text{resolution: } & r = \gamma ^ \phi \ \text{s.t. } & \alpha \cdot \beta ^2 \cdot \gamma ^ 2 \approx 2 \ & \alpha \ge 1, \beta \ge 1, \gamma \ge 1 \end{aligned}\tag{2} $

where $\alpha, \beta, \gamma$ are constants that can be determined by a small grid search. Intuitively, $\phi$ is a user-specified coefficient that controls how many more resources are available for model scaling, while $\alpha, \beta, \gamma$ specify how to assign these extra resources to network width, depth, and resolution respectively. Notably, the FLOPS of a regular convolution op is proportional to $d$, $w^2$, $r^2$, i.e., doubling network depth will double FLOPS, but doubling network width or resolution will increase FLOPS by four times. Since convolution ops usually dominate the computation cost in ConvNets, scaling a ConvNet with equation 2 will approximately increase total FLOPS by $\big(\alpha \cdot \beta ^2 \cdot \gamma ^2 \big)^\phi$. In this paper, we constraint $\alpha \cdot \beta ^2 \cdot \gamma ^ 2 \approx 2$ such that for any new $\phi$, the total FLOPS will approximately[^3] increase by $2^\phi$.

[^3]: FLOPS may differ from theoretical value due to rounding.

4. EfficientNet Architecture

Section Summary: EfficientNet starts with a compact baseline network called EfficientNet-B0, designed through a search process that balances high accuracy with low computational demands, using building blocks like mobile inverted bottlenecks enhanced with squeeze-and-excitation techniques. From this baseline, the model is scaled up efficiently by adjusting depth, width, and resolution in a coordinated way, first tuning coefficients on the small version and then applying them uniformly to create larger variants from B1 to B7. These scaled EfficientNet models achieve top performance on image recognition tasks while using far fewer parameters and computations than traditional networks, often reducing them by up to 8 times or more.

Since model scaling does not change layer operators $\mathcal{\hat F}_i$ in baseline network, having a good baseline network is also critical. We will evaluate our scaling method using existing ConvNets, but in order to better demonstrate the effectiveness of our scaling method, we have also developed a new mobile-size baseline, called EfficientNet.

Inspired by [9], we develop our baseline network by leveraging a multi-objective neural architecture search that optimizes both accuracy and FLOPS. Specifically, we use the same search space as [9], and use $ACC(m) \times [FLOPS(m)/T]^w$ as the optimization goal, where $ACC(m)$ and $FLOPS(m)$ denote the accuracy and FLOPS of model $m$, $T$ is the target FLOPS and $w$ =-0.07 is a hyperparameter for controlling the trade-off between accuracy and FLOPS. Unlike [9, 21], here we optimize FLOPS rather than latency since we are not targeting any specific hardware device. Our search produces an efficient network, which we name EfficientNet-B0. Since we use the same search space as [9], the architecture is similar to MnasNet, except our EfficientNet-B0 is slightly bigger due to the larger FLOPS target (our FLOPS target is 400M). Table 1 shows the architecture of EfficientNet-B0. Its main building block is mobile inverted bottleneck MBConv [7, 9], to which we also add squeeze-and-excitation optimization [12].

\begin{tabular}{c|c|c|c|c}  
    \toprule[0.15em]  
    Stage & Operator & Resolution & \#Channels & \#Layers \\
    $i$ & $\mathcal{ \hat F}_i$ & $ \hat H_i \times \hat W_i $ & $ \hat C_i$ & $ \hat L_i$ \\
    \midrule  
    1 & Conv3x3 & $ 224 \times 224 $ & 32 & 1 \\
    2 & MBConv1, k3x3 & $112 \times 112 $ & 16 &1 \\
    3 & MBConv6, k3x3 & $112 \times 112$ & 24 & 2 \\
    4 & MBConv6, k5x5 & $56 \times 56$ & 40 & 2 \\
    5 & MBConv6, k3x3 & $28 \times 28 $ & 80 & 3 \\
    6 & MBConv6, k5x5 & $14 \times 14$ & 112 & 3 \\
    7 & MBConv6, k5x5 & $14 \times 14$ & 192 & 4 \\
    8 & MBConv6, k3x3 & $7 \times 7$ & 320 & 1 \\
    9 & Conv1x1 \& Pooling \& FC & $7 \times 7$ & 1280 & 1 \\  
    \bottomrule[0.15em]  
\end{tabular}

Starting from the baseline EfficientNet-B0, we apply our compound scaling method to scale it up with two steps:

• STEP 1: we first fix $\phi=1$, assuming twice more resources available, and do a small grid search of $\alpha, \beta, \gamma$ based on Equation 1 and 2. In particular, we find the best values for EfficientNet-B0 are $\alpha=1.2, \beta=1.1, \gamma=1.15$, under constraint of $\alpha \cdot \beta ^2 \cdot \gamma^2 \approx 2$.
• STEP 2: we then fix $\alpha, \beta, \gamma$ as constants and scale up baseline network with different $\phi$ using Equation 2, to obtain EfficientNet-B1 to B7 (Details in Table 2).

Notably, it is possible to achieve even better performance by searching for $\alpha, \beta, \gamma$ directly around a large model, but the search cost becomes prohibitively more expensive on larger models. Our method solves this issue by only doing search once on the small baseline network (step 1), and then use the same scaling coefficients for all other models (step 2).

\begin{tabular}{l|cc||cc||cc}
  \toprule [0.15em]
  Model & Top-1 Acc. & Top-5 Acc. & \#Params & Ratio-to-EfficientNet &\#FLOPs & Ratio-to-EfficientNet \\
  \midrule [0.1em]
  \bf EfficientNet-B0 & \bf 77.1\% & \bf 93.3\% & \bf 5.3M & \bf 1x & \bf 0.39B & \bf 1x \\
  ResNet-50 [1] & 76.0\% & 93.0\% & 26M & 4.9x & 4.1B & 11x \\
  DenseNet-169 [24] & 76.2\% & 93.2\% & 14M & 2.6x & 3.5B & 8.9x \\

  \midrule
  \bf EfficientNet-B1 & \bf 79.1\% & \bf 94.4\% & \bf 7.8M & \bf 1x & \bf 0.70B & \bf 1x \\
  ResNet-152 [1] & 77.8\% & 93.8\% & 60M & 7.6x & 11B & 16x \\
  DenseNet-264 [24] & 77.9\% & 93.9\% & 34M & 4.3x & 6.0B & 8.6x \\
  Inception-v3 [25] & 78.8\% & 94.4\% & 24M & 3.0x & 5.7B & 8.1x \\
  Xception [32] & 79.0\% & 94.5\% & 23M & 3.0x & 8.4B & 12x \\

  \midrule
  \bf EfficientNet-B2 & \bf 80.1\% & \bf 94.9\% & \bf 9.2M & \bf 1x & \bf 1.0B & \bf 1x \\
  Inception-v4 [33] & 80.0\% & 95.0\% & 48M & 5.2x & 13B & 13x \\
  Inception-resnet-v2 [33] & 80.1\% & 95.1\% & 56M & 6.1x & 13B & 13x \\

  \midrule
        \bf EfficientNet-B3 & \bf 81.6\% & \bf 95.7\% & \bf 12M & \bf 1x & \bf 1.8B & \bf 1x \\
        ResNeXt-101 [34] & 80.9\% & 95.6\% & 84M & 7.0x & 32B & 18x \\
        PolyNet [35] & 81.3\% & 95.8\% & 92M & 7.7x & 35B & 19x \\

        \midrule
        \bf EfficientNet-B4 & \bf 82.9\% & \bf 96.4\% & \bf 19M & \bf 1x & \bf 4.2B & \bf 1x \\
        SENet [12] & 82.7\% & 96.2\% & 146M & 7.7x & 42B & 10x \\
     NASNet-A [27] & 82.7\% & 96.2\% & 89M & 4.7x & 24B & 5.7x \\
     AmoebaNet-A [30] & 82.8\% & 96.1\% & 87M & 4.6x & 23B & 5.5x \\
     PNASNet [36] & 82.9\% & 96.2\% & 86M & 4.5x & 23B & 6.0x \\

        \midrule
        \bf EfficientNet-B5 & \bf 83.6\% & \bf 96.7\% & \bf 30M & \bf 1x & \bf 9.9B & \bf 1x \\
     AmoebaNet-C [37] & 83.5\% & 96.5\% & 155M & 5.2x & 41B & 4.1x \\

        \midrule
     \bf EfficientNet-B6 & \bf 84.0\% & \bf 96.8\% & \bf 43M & \bf 1x & \bf 19B & \bf 1x \\
        \midrule
        \bf EfficientNet-B7 & \bf 84.3\% & \bf 97.0\% & \bf 66M & \bf 1x & \bf 37B & \bf 1x \\
        GPipe [2] & 84.3\% & 97.0\% & 557M & 8.4x & - & - \\
  \bottomrule[0.15em]
  \multicolumn{7}{l}{ We omit ensemble and multi-crop models [12], or models pretrained on 3.5B Instagram images [38]. }
  \end{tabular}

5. Experiments

Section Summary: In the experiments section, researchers test their compound scaling method on popular image recognition models like MobileNets and ResNets, showing it boosts accuracy more effectively than scaling just one aspect like size or depth. They introduce EfficientNets, a new family of models scaled from a small baseline, which achieve high accuracy on the ImageNet dataset using far fewer computations and parameters than competitors, while also running much faster on standard hardware. On transfer learning tasks across various datasets, EfficientNets set new records for accuracy with up to ten times fewer parameters compared to previous top models.

\begin{tabular}{l|cc}  
  \toprule[0.15em]  
  Model & FLOPS & Top-1 Acc. \\  
     \midrule[0.12em]  
  Baseline MobileNetV1 [6] & 0.6B & 70.6\% \\
  \midrule[0.05em]
     Scale MobileNetV1 by width ($w$ =2) & 2.2B & 74.2\% \\
     Scale MobileNetV1 by resolution ($r$ =2)&2.2B & 72.7\% \\
     \bf compound scale ($\pmb d$ =1.4, $\pmb w$ =1.2, $\pmb r$ =1.3) & \bf 2.3B & \bf 75.6\% \\
     \midrule[0.15em]  
     Baseline MobileNetV2 [7] & 0.3B & 72.0\% \\
     \midrule[0.05em]
     Scale MobileNetV2 by depth ($d$ =4) & 1.2B & 76.8\% \\
     Scale MobileNetV2 by width ($w$ =2) & 1.1B & 76.4\% \\
     Scale MobileNetV2 by resolution ($r$ =2) & 1.2B & 74.8\% \\
     \bf MobileNetV2 compound scale & \bf 1.3B & \bf 77.4\% \\ 

  \midrule[0.15em]
     Baseline ResNet-50 [1] & 4.1B & 76.0\% \\
     \midrule[0.05em]
     Scale ResNet-50 by depth ($d$ =4) & 16.2B & 78.1\% \\
     Scale ResNet-50 by width ($w$ =2) & 14.7B & 77.7\% \\
     Scale ResNet-50 by resolution ($r$ =2) & 16.4B & 77.5\% \\
     \bf ResNet-50 compound scale & \bf 16.7B & \bf 78.8\% \\ 

  \bottomrule[0.15em]
  \end{tabular}

In this section, we will first evaluate our scaling method on existing ConvNets and the new proposed EfficientNets.

5.1 Scaling Up MobileNets and ResNets

As a proof of concept, we first apply our scaling method to the widely-used MobileNets [6, 7] and ResNet [1]. Table 3 shows the ImageNet results of scaling them in different ways. Compared to other single-dimension scaling methods, our compound scaling method improves the accuracy on all these models, suggesting the effectiveness of our proposed scaling method for general existing ConvNets.

:Table 4: Inference Latency Comparison – Latency is measured with batch size 1 on a single core of Intel Xeon CPU E5-2690.

	Acc. @ Latency		Acc. @ Latency
ResNet-152	77.8% @ 0.554s	GPipe	84.3% @ 19.0s
EfficientNet-B1	78.8% @ 0.098s	EfficientNet-B7	84.4% @ 3.1s
\bf Speedup	\bf 5.7x	\bf Speedup	\bf 6.1x

\begin{tabular}{l||cccccc||cccccc}  
  \toprule [0.15em]
  & \multicolumn{6}{c}{Comparison to best public-available results} & \multicolumn{6}{c}{Comparison to best reported results} \\
  & Model & Acc. & \#Param & Our Model & Acc. & \#Param(ratio) & Model & Acc. & \#Param & Our Model & Acc. & \#Param(ratio) \\
  \midrule [0.1em]
CIFAR-10 & NASNet-A & 98.0\% & 85M & EfficientNet-B0 & 98.1\% & 4M (21x) & $^\dagger$Gpipe & \bf 99.0\% & 556M & EfficientNet-B7 & 98.9\% & 64M (8.7x) \\

CIFAR-100 & NASNet-A & 87.5\% & 85M & EfficientNet-B0 & 88.1\% & 4M (21x) & Gpipe & 91.3\% & 556M & EfficientNet-B7 & \bf 91.7\% & 64M (8.7x) \\

Birdsnap & Inception-v4 & 81.8\% & 41M & EfficientNet-B5 & 82.0\% & 28M (1.5x) & GPipe & 83.6\% & 556M & EfficientNet-B7 & \bf 84.3\% & 64M (8.7x) \\

Stanford Cars & Inception-v4 & 93.4\% & 41M & EfficientNet-B3 & 93.6\% & 10M (4.1x) & $^\ddagger$DAT & \bf 94.8\%& - & EfficientNet-B7 & 94.7\% & - \\

Flowers & Inception-v4 & 98.5\% & 41M & EfficientNet-B5 & 98.5\% & 28M (1.5x) & DAT & 97.7\% & - & EfficientNet-B7 & \bf 98.8\% & - \\

FGVC Aircraft & Inception-v4 & 90.9\% & 41M & EfficientNet-B3 & 90.7\% & 10M (4.1x) & DAT & 92.9\% & - & EfficientNet-B7 & \bf 92.9\% & - \\

Oxford-IIIT Pets & ResNet-152 & 94.5\% & 58M & EfficientNet-B4 & 94.8\% & 17M (5.6x) & GPipe & \bf 95.9\% & 556M & EfficientNet-B6 & 95.4\% & 41M (14x) \\

Food-101 & Inception-v4 & 90.8\% & 41M & EfficientNet-B4 & 91.5\% & 17M (2.4x) & GPipe & 93.0\% & 556M & EfficientNet-B7 & \bf 93.0\% & 64M (8.7x) \\
\midrule
  Geo-Mean & & & & & & \bf (4.7x) & & & & & & \bf (9.6x)\\
  \bottomrule[0.15em]
  \multicolumn{13}{l}{ $^\dagger$GPipe [2] trains giant models with specialized pipeline parallelism library.} \\
  \multicolumn{13}{l}{ $^\ddagger$DAT denotes domain adaptive transfer learning [39]. Here we only compare ImageNet-based transfer learning results. } \\
  \multicolumn{13}{l}{ Transfer accuracy and \#params for NASNet [27], Inception-v4 [33], ResNet-152 [1] are from [13]. } \\
  \end{tabular}

5.2 ImageNet Results for EfficientNet

We train our EfficientNet models on ImageNet using similar settings as [9]: RMSProp optimizer with decay 0.9 and momentum 0.9; batch norm momentum 0.99; weight decay 1e-5; initial learning rate 0.256 that decays by 0.97 every 2.4 epochs. We also use SiLU (Swish-1) activation [40, 41, 42], AutoAugment [37], and stochastic depth [43] with survival probability 0.8. As commonly known that bigger models need more regularization, we linearly increase dropout [44] ratio from 0.2 for EfficientNet-B0 to 0.5 for B7. We reserve 25K randomly picked images from the training set as a minival set, and perform early stopping on this minival; we then evaluate the early-stopped checkpoint on the original validation set to report the final validation accuracy.

Table 2 shows the performance of all EfficientNet models that are scaled from the same baseline EfficientNet-B0. Our EfficientNet models generally use an order of magnitude fewer parameters and FLOPS than other ConvNets with similar accuracy. In particular, our EfficientNet-B7 achieves 84.3% top1 accuracy with 66M parameters and 37B FLOPS, being more accurate but 8.4x smaller than the previous best GPipe [2]. These gains come from both better architectures, better scaling, and better training settings that are customized for EfficientNet.

Figure 1 and Figure 5 illustrates the parameters-accuracy and FLOPS-accuracy curve for representative ConvNets, where our scaled EfficientNet models achieve better accuracy with much fewer parameters and FLOPS than other ConvNets. Notably, our EfficientNet models are not only small, but also computational cheaper. For example, our EfficientNet-B3 achieves higher accuracy than ResNeXt-101 [34] using 18x fewer FLOPS.

To validate the latency, we have also measured the inference latency for a few representative CovNets on a real CPU as shown in Table 4, where we report average latency over 20 runs. Our EfficientNet-B1 runs 5.7x faster than the widely used ResNet-152, while EfficientNet-B7 runs about 6.1x faster than GPipe [2], suggesting our EfficientNets are indeed fast on real hardware.

5.3 Transfer Learning Results for EfficientNet

:Table 6: Transfer Learning Datasets.

Dataset	Train Size	Test Size	#Classes
CIFAR-10 [46]	50, 000	10, 000	10
CIFAR-100 [46]	50, 000	10, 000	100
Birdsnap [47]	47, 386	2, 443	500
Stanford Cars [48]	8, 144	8, 041	196
Flowers [49]	2, 040	6, 149	102
FGVC Aircraft [50]	6, 667	3, 333	100
Oxford-IIIT Pets [51]	3, 680	3, 369	37
Food-101 [52]	75, 750	25, 250	101

We have also evaluated our EfficientNet on a list of commonly used transfer learning datasets, as shown in Table 6. We borrow the same training settings from [13] and [2], which take ImageNet pretrained checkpoints and finetune on new datasets.

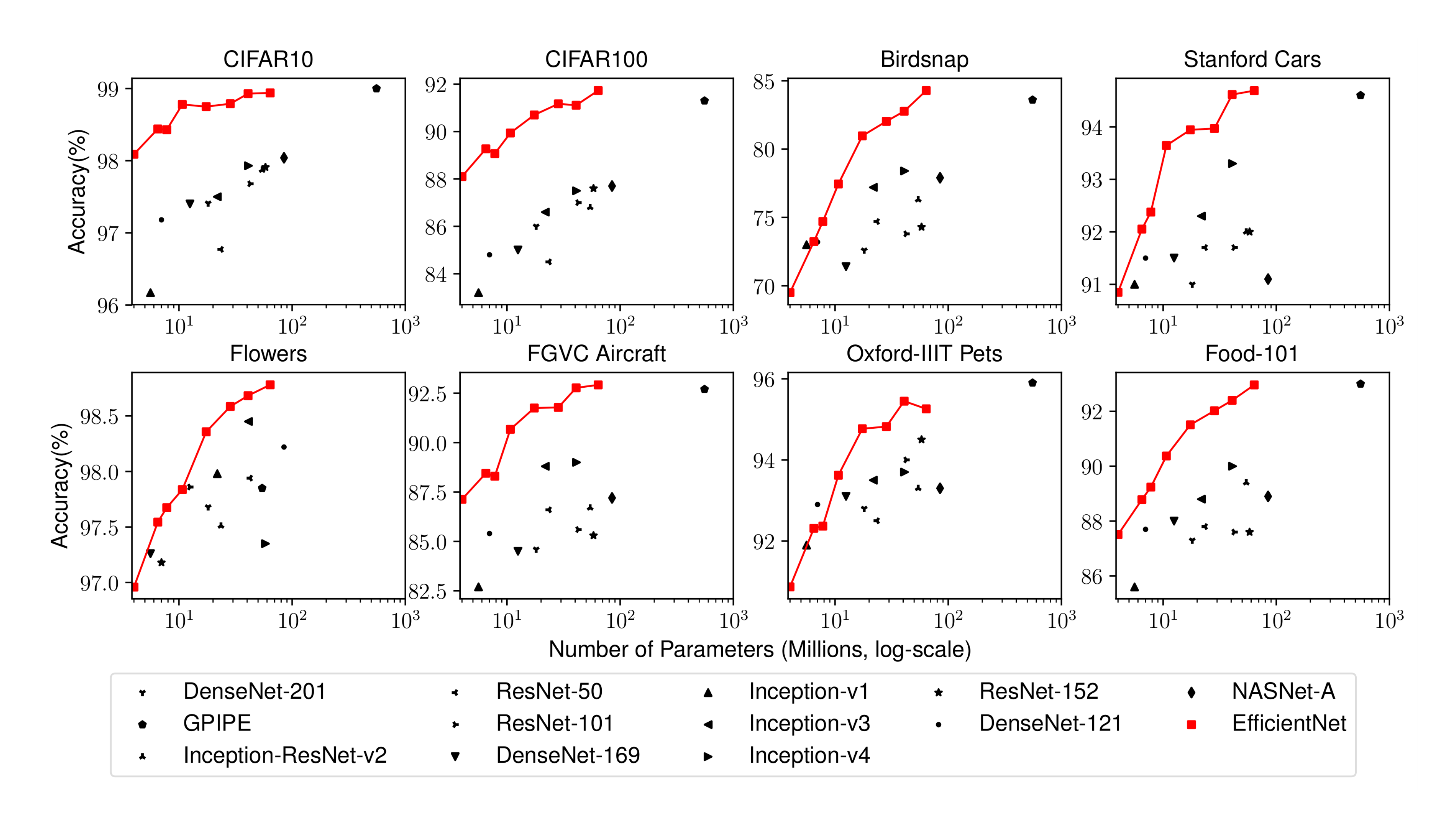
Table 5 shows the transfer learning performance: (1) Compared to public available models, such as NASNet-A [27] and Inception-v4 [33], our EfficientNet models achieve better accuracy with 4.7x average (up to 21x) parameter reduction. (2) Compared to state-of-the-art models, including DAT [39] that dynamically synthesizes training data and GPipe [2] that is trained with specialized pipeline parallelism, our EfficientNet models still surpass their accuracy in 5 out of 8 datasets, but using 9.6x fewer parameters

Figure 6 compares the accuracy-parameters curve for a variety of models. In general, our EfficientNets consistently achieve better accuracy with an order of magnitude fewer parameters than existing models, including ResNet [1], DenseNet [24], Inception [33], and NASNet [27].

6. Discussion

Section Summary: This section discusses how different ways of enlarging the EfficientNet-B0 model affect its performance on image recognition tasks using the ImageNet dataset. While scaling the model by increasing its depth, width, or resolution all boost accuracy but require more computing power, the proposed compound scaling method—which adjusts all three dimensions together—achieves up to 2.5% higher accuracy than the others for similar resource use. Visual comparisons of the models' focus on images reveal that compound scaling better highlights key object details and relevant areas, unlike the single-scaling approaches that often miss important parts or lack sharpness.

\begin{tabular}{l|cc}  
  \toprule[0.15em]  
  Model & FLOPS & Top-1 Acc. \\  
     \midrule[0.1em]  
  Baseline model (EfficientNet-B0) & 0.4B & 77.3\% \\
  \midrule
  Scale model by depth ($d$ =4) & 1.8B & 79.0\% \\
     Scale model by width ($w$ =2) & 1.8B & 78.9\% \\
     Scale model by resolution ($r$ =2) & 1.9B & 79.1\% \\
     \bf Compound Scale ($\pmb d$ =1.4, $\pmb w$ =1.2, $\pmb r$ =1.3) & \bf 1.8B & \bf 81.1\% \\ 
  \bottomrule[0.15em]  
  \end{tabular}

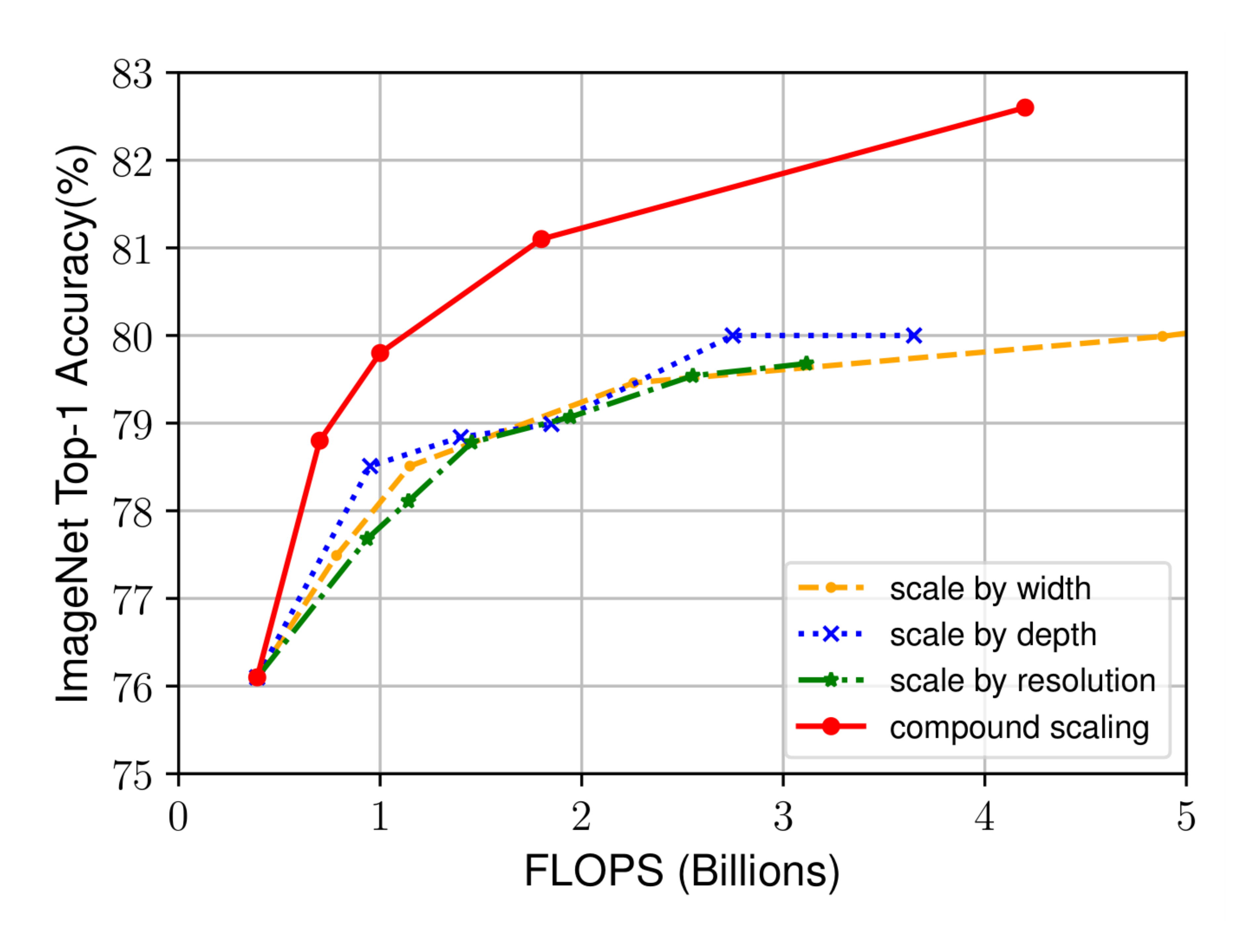
To disentangle the contribution of our proposed scaling method from the EfficientNet architecture, Figure 8 compares the ImageNet performance of different scaling methods for the same EfficientNet-B0 baseline network. In general, all scaling methods improve accuracy with the cost of more FLOPS, but our compound scaling method can further improve accuracy, by up to 2.5%, than other single-dimension scaling methods, suggesting the importance of our proposed compound scaling.

In order to further understand why our compound scaling method is better than others, Figure 7 compares the class activation map [45] for a few representative models with different scaling methods. All these models are scaled from the same baseline, and their statistics are shown in Table 7. Images are randomly picked from ImageNet validation set. As shown in the figure, the model with compound scaling tends to focus on more relevant regions with more object details, while other models are either lack of object details or unable to capture all objects in the images.

7. Conclusion

Section Summary: This paper examines how to scale up convolutional neural networks and finds that properly balancing the network's width, depth, and input resolution is a key factor often overlooked, which limits improvements in accuracy and efficiency. To fix this, the authors introduce a straightforward compound scaling method that allows scaling a basic network to fit any resource limits while preserving efficiency. Using this approach, they show that a compact EfficientNet model outperforms leading alternatives on ImageNet and five transfer learning datasets, but with far fewer parameters and computations.

In this paper, we systematically study ConvNet scaling and identify that carefully balancing network width, depth, and resolution is an important but missing piece, preventing us from better accuracy and efficiency. To address this issue, we propose a simple and highly effective compound scaling method, which enables us to easily scale up a baseline ConvNet to any target resource constraints in a more principled way, while maintaining model efficiency. Powered by this compound scaling method, we demonstrate that a mobile-size EfficientNet model can be scaled up very effectively, surpassing state-of-the-art accuracy with an order of magnitude fewer parameters and FLOPS, on both ImageNet and five commonly used transfer learning datasets.

Acknowledgements

Section Summary: The acknowledgements section expresses thanks to a group of researchers and engineers who provided help in the project. It specifically recognizes individuals like Ruoming Pang, Vijay Vasudevan, Alok Aggarwal, Barret Zoph, and others from the Google Brain team, including notable figures such as Samy Bengio and Jeff Dean. Their contributions were essential to the work's success.

We thank Ruoming Pang, Vijay Vasudevan, Alok Aggarwal, Barret Zoph, Hongkun Yu, Jonathon Shlens, Raphael Gontijo Lopes, Yifeng Lu, Daiyi Peng, Xiaodan Song, Samy Bengio, Jeff Dean, and the Google Brain team for their help.

Appendix

Section Summary: This appendix notes that since 2017, most studies on image recognition, including this one, have focused on comparing models using validation accuracy from the ImageNet dataset, a large collection of labeled photos. The authors went further by submitting their model's predictions on a separate test set to the official ImageNet website, confirming in Table 8 that the test accuracies closely match the validation ones across various model sizes from B0 to B7. The section ends with a list of references to foundational papers on neural networks and related techniques.

Since 2017, most research papers only report and compare ImageNet validation accuracy; this paper also follows this convention for better comparison. In addition, we have also verified the test accuracy by submitting our predictions on the 100k test set images to http://image-net.org; results are in Table 8. As expected, the test accuracy is very close to the validation accuracy.

\begin{tabular}{r|cccccccc}
  \toprule[0.15em]
  & B0 & B1 & B2 & B3 & B4 & B5 & B6 & B7 \\
  \midrule[0.1em]
  Val top1 & 77.11 & 79.13 & 80.07 & 81.59 & 82.89 & 83.60 & 83.95 & 84.26 \\
  Test top1 & 77.23 & 79.17 & 80.16 & 81.72 & 82.94 & 83.69 & 84.04 & 84.33 \\
  \midrule[0.1em]
  Val top5 & 93.35 & 94.47 & 94.90 & 95.67 & 96.37 & 96.71 & 96.76 & 96.97 \\
  Test top5 & 93.45 & 94.43 & 94.98 & 95.70 & 96.27 & 96.64 & 96.86 & 96.94 \\
  \bottomrule[0.1em]
  \end{tabular}

References

[1] He, K., Zhang, X., Ren, S., and Sun, J. Deep residual learning for image recognition. CVPR, pp.\ 770–778, 2016.

[2] Huang, Y., Cheng, Y., Chen, D., Lee, H., Ngiam, J., Le, Q. V., and Chen, Z. Gpipe: Efficient training of giant neural networks using pipeline parallelism. arXiv preprint arXiv:1808.07233, 2018.

[3] Zagoruyko, S. and Komodakis, N. Wide residual networks. BMVC, 2016.

[4] Raghu, M., Poole, B., Kleinberg, J., Ganguli, S., and Sohl-Dickstein, J. On the expressive power of deep neural networks. ICML, 2017.

[5] Lu, Z., Pu, H., Wang, F., Hu, Z., and Wang, L. The expressive power of neural networks: A view from the width. NeurIPS, 2018.

[6] Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D., Wang, W., Weyand, T., Andreetto, M., and Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv preprint arXiv:1704.04861, 2017.

[7] Sandler, M., Howard, A., Zhu, M., Zhmoginov, A., and Chen, L.-C. Mobilenetv2: Inverted residuals and linear bottlenecks. CVPR, 2018.

[8] Zoph, B. and Le, Q. V. Neural architecture search with reinforcement learning. ICLR, 2017.

[9] Tan, M., Chen, B., Pang, R., Vasudevan, V., Sandler, M., Howard, A., and Le, Q. V. MnasNet: Platform-aware neural architecture search for mobile. CVPR, 2019.

[10] Krizhevsky, A., Sutskever, I., and Hinton, G. E. Imagenet classification with deep convolutional neural networks. In NIPS, pp.\ 1097–1105, 2012.

[11] Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V., and Rabinovich, A. Going deeper with convolutions. CVPR, pp.\ 1–9, 2015.

[12] Hu, J., Shen, L., and Sun, G. Squeeze-and-excitation networks. CVPR, 2018.

[13] Kornblith, S., Shlens, J., and Le, Q. V. Do better imagenet models transfer better? CVPR, 2019.

[14] Han, S., Mao, H., and Dally, W. J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. ICLR, 2016.

[15] He, Y., Lin, J., Liu, Z., Wang, H., Li, L.-J., and Han, S. Amc: Automl for model compression and acceleration on mobile devices. ECCV, 2018.

[16] Yang, T.-J., Howard, A., Chen, B., Zhang, X., Go, A., Sze, V., and Adam, H. Netadapt: Platform-aware neural network adaptation for mobile applications. ECCV, 2018.

[17] Iandola, F. N., Han, S., Moskewicz, M. W., Ashraf, K., Dally, W. J., and Keutzer, K. Squeezenet: Alexnet-level accuracy with 50x fewer parameters and

lt;$0.5 mb model size. arXiv preprint arXiv:1602.07360, 2016.

[18] Gholami, A., Kwon, K., Wu, B., Tai, Z., Yue, X., Jin, P., Zhao, S., and Keutzer, K. Squeezenext: Hardware-aware neural network design. ECV Workshop at CVPR'18, 2018.

[19] Zhang, X., Zhou, X., Lin, M., and Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. CVPR, 2018.

[20] Ma, N., Zhang, X., Zheng, H.-T., and Sun, J. Shufflenet v2: Practical guidelines for efficient cnn architecture design. ECCV, 2018.

[21] Cai, H., Zhu, L., and Han, S. Proxylessnas: Direct neural architecture search on target task and hardware. ICLR, 2019.

[22] Lin, H. and Jegelka, S. Resnet with one-neuron hidden layers is a universal approximator. NeurIPS, pp.\ 6172–6181, 2018.

[23] Sharir, O. and Shashua, A. On the expressive power of overlapping architectures of deep learning. ICLR, 2018.

[24] Huang, G., Liu, Z., Van Der Maaten, L., and Weinberger, K. Q. Densely connected convolutional networks. CVPR, 2017.

[25] Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna, Z. Rethinking the inception architecture for computer vision. CVPR, pp.\ 2818–2826, 2016.

[26] Ioffe, S. and Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. ICML, pp.\ 448–456, 2015.

[27] Zoph, B., Vasudevan, V., Shlens, J., and Le, Q. V. Learning transferable architectures for scalable image recognition. CVPR, 2018.

[28] He, K., Gkioxari, G., Dollár, P., and Girshick, R. Mask r-cnn. ICCV, pp.\ 2980–2988, 2017.

[29] Lin, T.-Y., Dollár, P., Girshick, R., He, K., Hariharan, B., and Belongie, S. Feature pyramid networks for object detection. CVPR, 2017.

[30] Real, E., Aggarwal, A., Huang, Y., and Le, Q. V. Regularized evolution for image classifier architecture search. AAAI, 2019.

[31] Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bernstein, M., et al. Imagenet large scale visual recognition challenge. International Journal of Computer Vision, 115(3):211–252, 2015.

[32] Chollet, F. Xception: Deep learning with depthwise separable convolutions. CVPR, pp.\ 1610–02357, 2017.

[33] Szegedy, C., Ioffe, S., Vanhoucke, V., and Alemi, A. A. Inception-v4, inception-resnet and the impact of residual connections on learning. AAAI, 4:12, 2017.

[34] Xie, S., Girshick, R., Dollár, P., Tu, Z., and He, K. Aggregated residual transformations for deep neural networks. CVPR, pp.\ 5987–5995, 2017.

[35] Zhang, X., Li, Z., Loy, C. C., and Lin, D. Polynet: A pursuit of structural diversity in very deep networks. CVPR, pp.\ 3900–3908, 2017.

[36] Liu, C., Zoph, B., Shlens, J., Hua, W., Li, L.-J., Fei-Fei, L., Yuille, A., Huang, J., and Murphy, K. Progressive neural architecture search. ECCV, 2018.

[37] Cubuk, E. D., Zoph, B., Mane, D., Vasudevan, V., and Le, Q. V. Autoaugment: Learning augmentation policies from data. CVPR, 2019.

[38] Mahajan, D., Girshick, R., Ramanathan, V., He, K., Paluri, M., Li, Y., Bharambe, A., and van der Maaten, L. Exploring the limits of weakly supervised pretraining. arXiv preprint arXiv:1805.00932, 2018.

[39] Ngiam, J., Peng, D., Vasudevan, V., Kornblith, S., Le, Q. V., and Pang, R. Domain adaptive transfer learning with specialist models. arXiv preprint arXiv:1811.07056, 2018.

[40] Ramachandran, P., Zoph, B., and Le, Q. V. Searching for activation functions. arXiv preprint arXiv:1710.05941, 2018.

[41] Elfwing, S., Uchibe, E., and Doya, K. Sigmoid-weighted linear units for neural network function approximation in reinforcement learning. Neural Networks, 107:3–11, 2018.

[42] Hendrycks, D. and Gimpel, K. Gaussian error linear units (gelus). arXiv preprint arXiv:1606.08415, 2016.

[43] Huang, G., Sun, Y., Liu, Z., Sedra, D., and Weinberger, K. Q. Deep networks with stochastic depth. ECCV, pp.\ 646–661, 2016.

[44] Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. Dropout: a simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1):1929–1958, 2014.

[45] Zhou, B., Khosla, A., Lapedriza, A., Oliva, A., and Torralba, A. Learning deep features for discriminative localization. CVPR, pp.\ 2921–2929, 2016.

[46] Krizhevsky, A. and Hinton, G. Learning multiple layers of features from tiny images. Technical Report, 2009.

[47] Berg, T., Liu, J., Woo Lee, S., Alexander, M. L., Jacobs, D. W., and Belhumeur, P. N. Birdsnap: Large-scale fine-grained visual categorization of birds. CVPR, pp.\ 2011–2018, 2014.

[48] Krause, J., Deng, J., Stark, M., and Fei-Fei, L. Collecting a large-scale dataset of fine-grained cars. Second Workshop on Fine-Grained Visual Categorizatio, 2013.

[49] Nilsback, M.-E. and Zisserman, A. Automated flower classification over a large number of classes. ICVGIP, pp.\ 722–729, 2008.

[50] Maji, S., Rahtu, E., Kannala, J., Blaschko, M., and Vedaldi, A. Fine-grained visual classification of aircraft. arXiv preprint arXiv:1306.5151, 2013.

[51] Parkhi, O. M., Vedaldi, A., Zisserman, A., and Jawahar, C. Cats and dogs. CVPR, pp.\ 3498–3505, 2012.

[52] Bossard, L., Guillaumin, M., and Van Gool, L. Food-101–mining discriminative components with random forests. ECCV, pp.\ 446–461, 2014.